由地转流公式可知，只要知道等压面相对等势面的倾角，就可计算地转流速。但是等压面的倾角量级大小，至今难以直接测量。因此只有借助于海洋调查中的温度、盐度和深度(压力)资料，根据海水状态方程，首先计算海水的密度或比容，进而计算等压面之间的位势差，再进行地转流的计算。

一、计算公式(海兰—汉森公式)

设在垂直于地转流向的铅直断面上取相距L的两个测站A0与B0，如图5－6所示。Φ0、Φ1、Φ2与p0，p1，p2分别为等势面与等压面，β0、β1、β2为等压面的倾角，v0、v1、v2分别为等压面p0、p1、p2上的流速，则

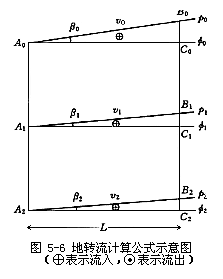
其中B1B2与A1A2分别为p1与p2等压面之间在B0与A0站的铅直几何距离，根据关系式

它们可以用位势差表示，则有

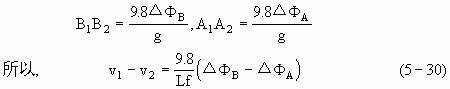
ΔΦB、ΔΦA分别为pl与p2等压面之间在B0与A0站的位势差。其计算方法由式(5—11)给出。

必须指出，由式(5－30)计算的流速是p1等压面相对p2等压面的流速，并非相对静止海底的绝对流速。同理可计算自海面至海底任何两等压面之间相对流速。

二、流速参考零面的选取

为求得各层相对海底的绝对流速，必须在海洋中选取一个流速为零的参考面。在大洋中这个面是可以找到的，具体方法读者可参考有关专门文献，本书不作进一步介绍。至于浅海中零面的选取，可近似地视海底为零面，然后对不同深度的海底进行订正即可。

由于动力计算方法是计算不同倾斜角度的两等压面之间的相对流速，所以它只适应于内压场引起的地转流的计算，对外压场导致的倾斜流，不能用此法进行计算。因为外压场中自表至底各等压面都是平行的，其倾角相同，因此各等压面之间的相对流速都为零。

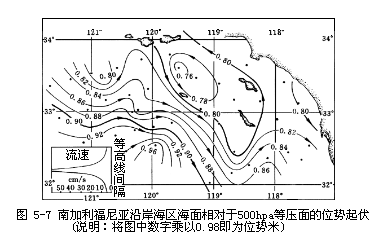
实际工作中，由于我们事先无法了解地转流向，在布设调查断面时难以与其垂直。因此，通常在调查海区中布设多个测站，然后根据调查资料计算每个测站相应等压面的位势差，据此绘制位势高度等值线(图5—7)。高值中心，表示等压面上凸，低值中心表示等压面下凹。根据压力场与流场的关系，不难理解这些等位势高度线就是地转流向线。在北半球，绕高值中心的流动方向为顺时针，绕低值中心的流动方向为反时针。在南半球相反。而且等位势高度线密集处流速大，稀疏处流速小。