相对小振幅波而言，有限振幅波具有较大振幅。它与实际海浪的形状更接近。有限振幅波动理论很多，例如斯托克斯波、摆线波、孤立波等，其理论推导多是繁杂的。为了与小振幅波作一比较，本节只简要介绍一下斯托克斯波理论的一些主要结论，不作进一步论证。

6.3.1斯托克斯波的波剖面

该波剖面不是简谐曲线，它对于横轴上下不是对称的，水质点的振动中

6.3.2波速与波高

有限振幅波速不仅与波长有关，而且与波高有关。当波陡，即波高与波长之比愈大时，波速也愈大。其波速的近似公式为

可见其波速略大于小振幅波。由上式可以看出，当波高与波长之比(δ＝H/λ)很小时，式(6—21)便蜕变为小振幅波速的形式。

6.3.3水质点运动轨迹

水质点的运动轨迹与小振幅波动中的运动轨迹相似，接近为圆，但在一个周期内不是封闭的。其水平方向与铅直方向上的位移变化分别为

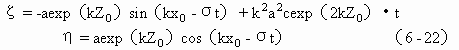
上式说明水质点在一个周期内，水平方向上向前存在一个净位移

移称为“波流”，可用以解释在波浪传播方向上导致的海水运输现象。不难计算，跨过单位波峰线宽度，自表至波动消失处，单位时间内，由于波流运输的海水体积为

波流对海流、波浪的成长以及泥沙的输运都具有一定的影响。

6.3.4波动的能量

小振幅波中，波动的动能与势能相等，但对斯托克斯波而言并不相等，而是Ek＞Ep，即动能大于势能；还可证明，在铅直方向上波动的动能大于水平方向上的动能。

6.3.5波动的振幅与波高

当波动的振幅(从而波高)相对波长之比超过一定限度时，波面将破碎，

就会破碎。小振幅波理论尚不能解释实际海浪的破碎现象。