师:你们小组拼成的图形怎么是正方形呢?请到台上说说看。
生5:我们准备的平行四边形底和高相等,所以通过割补后就成了正方形(图4),根据正方形面积的计算方法同样可以推导出平行四边形面积的计算方法。
师:太妙了!还有没有别的方法呢?
生6:我们小组在画平行四边形的高时,将平行四边形分成两个直角三角形,把这两千三角形拼起来,就成了一个长方形(图5),这样同样可以推导出平行四边形面积的计算方法。
师:你们真聪明,从不同角度探索平行四边形面积的计算方法,不但想得深,学得透,而且还注意探索新方法,新思路,真了不起!
师:怎样用字母来表示这个公式呢?
生1:如果用S表示平行四边形的面积,用a表示平行四边形的底,用h表示平行四边形的高,那么平行f四边形面积的计算公式可以写成S=a×h。
生2:S=a×h可以写成S=a。h或S=ah。
师:为什么?
生:因为在含有字母的式子里,字母和字母中间的乘号可以记作"。",也可以省略不写。
[评析:学生有疑之后,教者给予充分的时间、空间,让学生借助学具,动手操作,自己探索平行四边形面积的计算方法。这一过程,学生议论纷纷,各抒己见,主体地位发挥得淋漓尽致,闪烁着创新的火花。教师寥寥数语,点拨适度,顺着学生的学习思路有序展开教学。]
三、巩固深化,发展智能
师:回答得很好!刚才我们对图形进行剪、移、拼,时找到了计算平行四边形面积的方法,现在你们想用这个知识解决一些实际问题吗?
师:(投影出示)请大家做两道题。
1.一块平行四边形钢板(如下图),它的面积是多少?(得数保留整数)
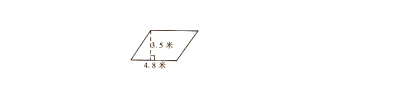
2.判断题。(请各组先讨论,再判断。)
①把一个平行四边形割补成长方形,它们的面积相等。
②一个平行四边形的底是7分米,高是4分米,面积是28分米。
③一个平行四边形的底是5米,高是2分米,面积是100平方分米。
师:刚才你们猜这个平行四边形(指导人新课时的框架)的面积时,出现了两种答案,到底哪种答案正确呢?
生:比6平方分米小。
师:请你说说理由!
生:通过比较,我发现平行四边形的底与长方形的长相等,平行四边形的高比长方形的宽短,所以平行四边形的面积一定比6平方分米小。
师:你们同意这位同学的看法吗?
生:(通过几秒深思)点头默许。
师:长方形拉成平行四边形后,除了面积变小外,你们还发现了什么?
生1:形状变了。
生2:面积和形状变了,但周长不变。
师:你能说说原因吗?
生:因为长方形拉成平行四边形后,四条边的长度没有发生变化。
师:通过刚才的探索、学习,你们还有什么疑问?
生1:长方形框架拉成平行四边形后,面积变了,而我们刚才推导平行四边形面积公式时,为什么拼成的长方形的面积与原来平行四边形的面积会相等呢?
师:这个问题提得很好!谁愿意帮她?
生:我们刚才推导平行四边形面积的计算公式时,拼成的长方形的长、宽分别与原来平行四边形的底、高相等。所以它们的面积也相等。而长方形框架拉成平行四边形后,高变了,所以面积也就变了。
师:这位同学回答得真棒,我们用热烈的掌声给予祝贺!
[评析:练习设计由浅入深,层层递进,与导入新课时的疑点联系起来,首尾呼应,浑然一体,既巩固所学内容,又深化新知,更重要的是学生在练习中思维得以发展,创新素质得到锤炼。]
四、总结全课,提高认识
师:这节课我们学习了什么知识?是怎么来学会这个知识的?


