二、地球的大小

　　地球是一个球体。一个球体的大小，通常是用它的半径、周长以及表面积来表示的。

　　宇航技术的迅速发展、已使人们获得了有关地球大小的相当精确的数据。1979年，根据大地测量，地球物理协会决定，采用下列数据来表示地球的大小：

　　地球的赤道半径（a）：6378.137千米；

　　地球的极半径（b）：6356.752千米；

　　地球的赤道周长（2πR）：40075.7千米；

　　地球的表面积（4πR²）：510100934平方千米。

　　对于地球大小的认识，同样是经历了漫长的过程。随着科学技术的不断发展，人们越来越精确地了解到地球的大小。

　　古希腊的埃拉托色尼，是世界上最早用科学的方法测算地球大小数据的天文学家。他认为，地球是个球体，平行的太阳光在正午时照射到同一经线的不同地点，会与地面形成不同的交角。这样，便可对地球经线的弧度和每度弧长进行测算。

　　公元前200多年，埃拉托色尼进行了关于地球大小的直接测算。他选定大致位于同一经线上的赛恩（今阿斯旺附近）和亚历山大城为观测地点，在夏至日的正午，观测太阳光对地面的照射情况。在赛恩，太阳光可以直射到深井的底部，说明此时太阳光垂直照射地面，即太阳光线与当地铅垂线之间的夹角为0°；而在亚历山大城，同一时刻太阳光并不垂直照射地面，太阳光线与当地铅垂线之间有7°12′的夹角。显然，7°12′也就是赛恩与亚历山大城之间的纬度差。而这一角度（两地之间的纬度差）又恰好等于一个圆周（360°）的1/50。埃拉托色尼测量了上述两地之间的实际距离。然后，根据这些实测数据，用数学计算的方法求得了该经线圈的周长和半径。埃拉托色尼是把地球视为正球体的，所以，这个经圈的半径，也就是地球的半径。根据这个半径，进而计算出地球表面积等数据（图6-4）。

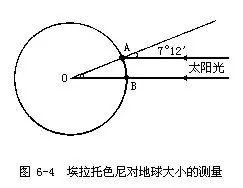
　　埃拉托色尼在两千多年前测算出的地球半径约为6200～7300千米。这一数据与现代实测的结果，已经相当近似。他在测量中所运用的基本方法和原理，一直为后人所沿用。直到近代的大地测量工作，也仍然运用这一基本原理，只是在测量纬度差时，所依据的观测天体不是太阳，而是距地球更加遥远的恒星，并运用三角测量的方法，测算地面上两地间的实际距离。宇宙间其它恒星与地球之间的距离，比太阳与地球的距离遥远得多，在地球上看来，太阳是一个圆面，而其它遥远的恒星都只是一个光点。因此，把非常遥远的恒星的光当作平行光，比把太阳光当作平行光，更加接近实际。再加上精密的观测仪器和先进的测算技术，所得到的测算结果，自然要比古人精确得多。