7．5 人口过程

人口过程一般包括人口增长过程和人口空间过程两方面，人口空间过程主要包括人口迁移和集聚过程，人口分布是空间过程的时间段面，也是地理学研究的重要内容．

7．5．1 人口增长过程

人口增长的早期模型是建立在人口随机生灭的假设前提上的．设人群在时刻t的人口数为n，时间[t，t+dt]内的生育概率为 λ(t)，死亡概率为 μ(t)，则 dt内人口增长速度为：

求解这个方程得：

(7．5．2)

如果λ＜μ，则人口趋于灭亡；如果λ＞μ，则人口无限增长，这就是著名的马尔萨斯(R．T．Malthus)学说．马尔萨斯过分地强调了人口增长的指数关系，而忽视了资源对人口的调节作用，是一种纯人口学的假说．

考虑资源限制对人口产生的主动与被动作用，对人口方程可以引入“最大允许人口数”N，这时(7．5．1)改作：

这个方程的解为：

(7．5．4)

在这个模型中，人口增长的上限是N，下限是零，这一模型称为Logistic模型或Verlhust模型．

上述方程并未考虑人口的年龄分布，实际上人口增长率主要是由育龄妇女的生育模式及总和生育率决定的，引入年龄结构的人口发展方程——Sharpe-Lotka方程，它是一个线性一阶初边值问题：

(7．5．5)

(7．5．6 )

这里l(a，t)表示t时刻的人口年龄分布密度，即a岁人口占t时刻总人口的比重，Φ(a)为初始人口年龄分布；k(a,t)表示t时刻a岁女性人口占a

岁人口的比重；β(a，t)表示t时刻a岁育龄妇女生育率，a1，a2分别为育龄区间的下限年龄和上限年龄；μ(a，t)表示t时刻a岁人口的死亡

总人口定义为：

A为人口寿命上限值或∞，方程(7．5．4)-(7．5．7)有形式解：

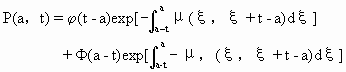
=P(t)l(a，t)

(7．5．9)

与μ(t)(t∈[t-a，t])近似呈负指数关系．

式(7．5．6)还可以进一步写成：

(7．5．10)

其中r(t)为总和生育率，h(a，t)为生育模式，宋健、于景元(1985)认为，h(a，t)对年龄服从Γ-分布：

(7．5．11)

式中α、θ为正参数，Γ(a)为Γ函数．

7．5．2 人口空间过程

1．人口分布

人口分布是人口地理学的核心内客之—．与所有的地理现象一样，人口分布是有地域分异特征的，一般讲自然环境的差异，决定了人口的本底分布，经济环境、尤其是城市的存在，产生了人口的再分布．另外，政治原因、国界的存在都对人口分布产生强烈的作用．

人口分布因素除了自然因素、社会因素外，还应看到历史的作用．在历史上某些民族因自然、社会、经济或战争因素而被迫迁移到特定地区，并且适应了当地的较恶劣的自然环境，也就出现了人口分布对正常状态的偏离．

关于人口分布规律，与我们观察的尺度有关，从球观的尺度看，距海岸线愈近人口愈密，但域观尺度上观察，海岸附近的人口反而小于稍远的地方(徐庆凤，1989)，“微观”上看，人口均集中于一个个居民点中，人口密度往往失去意义．

关于人口分布的因素尽管可以追溯到多方面，但就人口的最终分布来说，所有解说都只能是“哲理性”的而不是物理性的．由于影响人口分布因素的广泛性，要找出一种因素对人口密度差异或人口分布的数量上的精确关系，从根本上讲几乎不可能，研究的地域范围越小，越是如此．我们只能从宏观统计意义上谈论人口分布及其直接改变因子(生死过程、迁移过程)，而且我们承认人口分布的关系是复杂的、不确定的、宽容的．

在上述困扰下，关于人口分布的研究有时不得不就事论事，寻找人口分布的地区规律和表面特征，而关于形成原因的说法往往反为其次．Lorenz曲线就是表象分析的典型手段具体做法是，先按人口密度为序排列区域单元，然而沿X和Y轴同时按既定次序作出面积-人口累计频度坐标，连接这些点构成凸曲线，而该曲线与对角线之间的包络面积与上三角形面积之比，即为人口分布差异水平指标．图7．5．1是山东省胶东地区的人口分布Lorenz曲线，a、b两图对比，发现农村人口分布趋向均匀．(丁金宏，1989)

 

　

2

 

．人口迁移的一般理论

广义的人口迁移就是人口的空间位移，但是实际研究中我们往往要加上时空尺度的限制，因为严格地说人每时每刻都在发生着尺度不等的空间位移，人口地理学上定义的迁移与定居相辅相成，它通常是指人们改变自己定居点的过程，这种改变即使不是终生的，也至少在一年内不会重复原地定居．

人口迁移事件是在两个地点之间发生的，从迁移路线方向的总特征上我们可以将迁移分成几种类型：

(1)辐合型迁移：人口由多个迁出地向一个迁入地汇集，这种形式多发生在区位优越的城市或交通枢纽地区．

(2)辐散型迁移：人口由一个迁出地向四周发散，这种迁移多是由于灾发性因子(如灾害、水库建设等)产生的，也有的是环境特别险恶的局部地区，人口缓慢向外流迁．

(3)单向迁移：人口由一个区域稳定地向另一个区域迁移，这种迁移多是在广阔的地理背景下形成的，比如美国向西海岸的移民，我国历史上的三次南下迁移(这三次只是长期南下过程中相对集中的峰期)、华北闯关东、华南下南洋，以及解放以来我国先由东而西再由西而东的迁移．

(4)散射型迁移：迁移方向没有宏观趋向，近于随机，这种人口迁移多是由人们日常生活环节转移引致的，象儿童随父母的迁移、青年女性的婚姻迁移、老年人退休返乡等等．

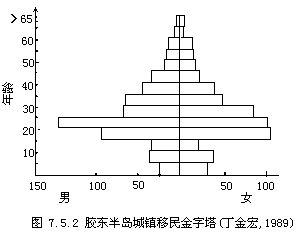
人口迁移率与年龄有明显关系，一般地说女性迁移多因婚姻，男性迁移多因就业．对比图7．5．2和7．5．3可以看出，我国迁移人口中，50—60岁的退休回返和10岁以下的儿童随迁并无峰态，而发达国家则峰势明显，这说明我国老年职工大多不愿放弃城市户口，而已婚育的青年男女不易外出就业，或只能只身出走，妻儿留居，所以儿童迁移率也不高．

在西方，人口迁移的原因一般被认为主要是经济上的，或者为了工作，或者为了居住条件．在社会主义国家，除了这种经济目的的迁移，还有政府组织和动员的非经济原因迁移，例如我国在“文革”期间为了“反修防修、巩固专政”组织了大规模的知识青年上山下乡运动．

从空间尺度来讲，迁移一般可分为地方性(local)、区际性(interregional)和国家性或国际性(international)三个层次，地方性和区域迁移一般呈现一定程度的距离衰减规律：

　

　

　

或

Mij=AiBjexp(-β·Dij)

(7．5．13)

式中，Mij表示地方i迁到地方j的迁移流强度或迁移率，Ai为地方i的推因子，Bj为地方j的拉因子，参数β＞0， r＞0，Dij为两地间距离，相对而言(7．5．12)式适合于地方迁移，(7．5．13)式适合于区域迁移．国家性(国际性)迁移往往受政治、经济影响较大，距离影响不明显．

为研究人口迁移对人口分布的影响，方程(7．5．5)被修改作：

(7．5．14)

这里f(a，t)是人口迁移函数．在考虑一个区域系统时，我们可以对每个亚区建立一个方程(7．5．14)，这样得到人口迁移与自然增长作用下的年龄-地区分布估计，这时用li、μi、fi作为i区的相应变量，显然，Σfi=0．

　

3．人口迁移的若干学说

　

人口迁移的理论研究比人口地理学的系统探索还要早，形成了多种迁移学说．

(1)Ravenstein的迁移定律

早在 1876年，E．G．Ravenstein在《地理分析》上发表了“出生地与迁移”的论文，1885，1889年，又先后在《统计学会杂志》上发表了“迁移定律”的长篇著述，Grigg总结了 Ravenstein的定律(Woods， 1979)，计11条：

①大多数迁移者只是短距离迁移；

②迁移过程是逐段的；

③长距离迁移者倾向于迁入大型工商业中心；

④每股迁移流产生一个补偿性对流；

⑤生长在城里的居民的迁移活性不如农村居民；

⑥在出生地小区域中女性人口的迁移活性大于男性，而外出闯荡的机会男性多于女性；

⑦多数迁移者为成人，其它家庭成员很少出县迁移；

⑧大城市的人口增长成分中迁移多于自然增长；

⑨迁移量随着工商业的发展和交通改善而增长；

⑩迁移的主要方向是从农村地区向工商业中心；

迁移的主要原因是经济．

(2)李的迁移三要素理论

由于Ravenstein的“迁移定律”高瞻远瞩，在他之后的几十年中，人口学者和地理学者都陷入“有景道不得”之境地，直到1966年E．S．Lee(据侯文若，1988)才提出迁移的三要素理论．

李首先科学定义了人口迁移的概念，李认为所谓人口迁移，就是指人们的居住地发生永久性或半永久性的变更，他把流浪者和到处觅求优厚待遇的流动工人排除在迁移者之外．李提出，每一次迁移活动必须具有三个相互联接的要素，这就是出发地或迁出地、目的地或迁入地、介于两者之间的中间障碍．

李认为，在迁出地总有一些因素引起人们的迁移动机，但也有一些因素阻止人们的这种念头，前者称为正因素，后者称为负因素．同样，在迁入地也总有一些正因素和负因素在发生作用，前后吸引人们迁入，后者则起反作用．人们决定是否迁移，主要取决于两地正负因素的对比．但他又指出，人们对迁出地的因素往往要多方面反复思考，不急于作出决定，但对迁入地的考虑往往只顾及一两个方面．迁移决策之后，人们还会受到中间障碍的考验，这些障碍包括距离、迁居费用、移民法规等，对富有者而言，前两种障碍不在话下，但有关移民法规确是难以逾越的．

李进一步论述了决定迁移规模的诸因子，如：迁入地与迁出地的差异、迁移者的内禀属性、中间障碍、经济周期、社会和经济发达程度等．

(3)Wolpert的地点效用理论

J．Wolpert 1965年首先提出地点效用论(张超、沈建法，1991)．地点效用的定义是个人对一个地点的满意或不满意程度．如果地点效用是可以量测的，那么可以发现不同的两个人对同一地点的效用是显著不同的，原因是各自的评价指标不一致．一个人对居住地的效用评价是比较确定的，因为他直接经历了当地生活的利弊，而他对其它地点的评价只能是以已经获得的信息为基础的一种预测．人口迁移的原因是人们认为在另一地的地点效用要高于原居住地．

(4)流动转变理论

流动转变理论是 W．Zelinsky 1971年提出的，他认为，随着社会的发展，同人口(增长)转变相对应，人口的流动性也会发生有规律的转变(Woods，1979)．根据流动转变理论，可以把社会发展分成五个阶段，即Ⅰ．传统社会，Ⅱ．早期转变社会，Ⅲ．后期转变社会，Ⅳ．发达社会和 Ⅴ．高度发达社会．不同的阶段对应不同的人口迁移特征．

在阶段Ⅰ，真正的迁移很少，只有有限的流动，起因于社会活动、地方性经济活动、战争和宗教．

在阶段Ⅱ，大规模流动开始发生，主要是农村向城市的迁移．这一阶段流动转变与工商业发展、城市兴起有密切关系，并产生深远影响．这一转变首先出现于英国，后来逐渐扩展到欧洲和世界各地，是不发达国家走向发达的起飞阶段的主要特征．在这一阶段的欧洲历史上，也出现了向美洲的大规模移民．

在阶段Ⅲ，农村向城市的迁移仍然非常重要，但开始减缓，国际移民也出现减少势头，但人口流动的规模和复杂性进一步增加．

　

　

在阶段Ⅳ，随着城市化的发展，城市之间和城市内部的迁移成为主要流动形式，随着生活水平提高和交通条件的改进(特别是私人汽车的普及)，人口流动继续增加．国际迁移主要有不发达国家普通劳工外迁和熟练劳动力、技术人员的迁移．

在阶段Ⅴ，几乎所有的永久迁移都是城市间或城市内部迁移．有些流动形式已经可以替代永久性迁移，而有些人口流动又进一步为通讯手段所代替，此人口流动会有所减少，当然目前尚没有哪个国家能完全属于这一阶段，在国家内部，象美国的南加利福尼亚日本的高度城市化地区等最接近这一状态．

图7．5．4表示各类流动在各阶段的变化，人口流动、城市内和城市间的迁移上升迅速而国际迁移、农村向城市的迁移以及向边远地区的迁移都是先升后降形成一个高峰．

　

7．5．3 人口空间过程的数学理论

　

1．流场理论

　

H．Hetelling(1978)在“迁移的数学理论”中提出，设土地是均质的，那么人口稀少的地方比人口稠密的地方有更好的生产条件，因此人口将从密度大的地方迁向密度小的地方．记P为人口密度，σ为区域人口饱和度，r为人口净增长率，β是一迁移常数，于是有方程：

在稳定流条件下，(7．5．15)式化作

Beckmann(1980)修改了Hetelling的模型基础，认为驱动人口流动的因子是工资W，故有流场

从而得

ΔW=-q(x，y，P，W)

(7．5．21)

式中，Δ是拉普拉斯算子．当P，W也作为x，y的函数时，(7．5．21)式满足泊松方程，在WU界区域有解：

(7．5．22)

然后由P与W的经验关系可以进一步估算人口流．

　

2．随机扩散理论

　

人口迁移的随机理论可以追溯到 Ravenstein 1885年的工作． 1970年 Wilson发展了这方面理论，提出了空间相互作用的最大熵模式． Kanaroglou Liaw和 Papageorgiou(1986)又系统地发展了这一理论．

这一理论构成了空间动力学的数学基础，我们已在第6．4节中叙述．其核心式(6．4．10)物理理解如下：

设空间有L个区域，N个人口，nj为第j个区域的人口数．由于存在空间相互作用，区域间人口将发生迁移．记qji(t)为t时刻区域j对区域i的相互作用强度，也就是说j区以qji的概率强度吸引i区人口，所以i区的人口单位时间内流向j区的量为qij(t)ni(t)．同理，j区人口也以qij(t)nj(t)的速率流向i区．j区与空间所有i(≠j)区作用的结果使得j区人口在单位时间的变化率满足

(7．5．23)

式(23)的写法考虑了第一、第二项中同时包含有qjjnj，时对对消，所以实际计算时，并不取i=j的情况，与物理上不考虑从j到j的“迁移”一致．

对于方程(7．5．23)，Grunbery和Modigliani(1954)证明有平衡解，也就是说不考虑人口增长时，人口空间系统可以达到平衡，不会出现过度聚集．

 

　

　　本文标题：人口过程-资源与人口
　　手机页面：http://m.dljs.net/dlsk/lidi/21117.html
　　本文地址：http://www.dljs.net/dlsk/lidi/21117.html