2.2 地表过程:漫流与径流
地表水的运动包括河川径流(汇流)、坡地(漫)流、蒸发、入渗等;后者主要是界面过程,我们已在上节讨论.控制地表水运动漫流与径流的基本方程是圣维南(Saint-Venant)方程,它是一般的流体运动方程的一维特殊形式:
连续性方程
![]()
动量方程
![]()
式中,x是沿流向的距离,V是断面平均流速,R是旁侧入流,它是汇入的流量,S0是流床坡降,Sf是流体的摩阻能坡即流体上表面坡降,h是水深,A是水流断面.为了解这组方程,需要补充关于A与h的关系
A=f(h)
(2.2.3)
并且常用流速V与h和能坡Sf的经验关系,所谓蓄泄关系替代(2.2.2)式,以使求解简化.
2.2.1 坡面漫流
1.基本理论
坡面漫流或漫流是降水在被植物截留、对地面填洼、下渗后余出的水量在地表坡面形成的一种水流.有时,也包括雨水在上坡段渗入在下部坡面段渗出形成的水流
在简化的情况下,坡面漫流被看作是一维的,定义x指向河道,这时坡面流满足一维Saint-Venant方程,从(2.2.1),(2.2.2)可以导出:

式中,q为单宽流量,h为水深,u为x方向单宽流速,S0为坡面坡降,Sf为阻力坡降,无量钢数,R为侧向入流,这里为降雨强度与渗入渗出坡面水量的代数和,g为重力加速度.
理论上利用Saint-Venant方程,可以用数值方式求出坡面上任意一点相应时刻的水深.实际上由于式(2.2.4),(2.2.5)是非线性的,数值方法求解也具有一定的困难性,因此发展了一些替代方法.
第一种替代方法是水文学方法或称水文学途径.注意到水量平衡等价于连续性方程,所以当以整个坡面为一水文系统时,取它的储水量为s,设坡长为L,则有
![]()
式中,q(L,t)为坡底(x=L)处的单宽出水量.进一步设单宽流量与h有关系
q(x,t)=bhα(x)
(2.2.7)
则可以令x=L,得到坡底处q(L,t)的与h的关系,代入(2.2.6)式,从而求出坡底漫流的动态.
另一种简化取(2.2.7)代替动量方程,并与连续性方程联立,这种途径称水力学途径,它包含了q是h的单值函数的假定,在某些情况下,这一假定并不合理.
理论分析发现,连续性方程和q-h的幂函数关系相当于将坡面流处理作运动波.实际上重写二式如下

![]()
![]()
成立,参数化c=dq/dh,则有
![]()
这个方程具有以c为相速的波动解,故称这种简化为运动波模型.
利用运动波模型,已经发现在坡面上漫流深度将上涨以达到特定的平衡水深,平衡时漫流流量与距离呈幂函数关系(文康等,1991)
![]()
或
![]()
这里b是某一特征.由于忽视入渗,所以漫流以R为上涨速度,坡长有限,故坡脚水深必然达到某一平衡水深,达到平衡水深的时间容易算出,为:
![]()
式中L为特征坡长.而雨止后退水历时td为

式中,tr为降水历时,ts为降水历时小于达到平衡水深时的一个特征时
![]()
2.入渗的作用:漫流的全部过程模拟
上述讨论避开了入渗的作用,并取R为常数,实际上漫流产生过程是复杂的,降水初期,由于土壤比较干燥,雨水趋于全部入渗.随着入渗时间的延入,土壤入渗率逐渐降低,降雨强度大于入渗强度的局域坡面开始产流,进而可能演化为整个坡面产流.
产流过程是复杂的,在湿润地区,可能以蓄满产流为主,即土壤饱和使地下水面达到地表而产流;在干旱地区,则可能因降水强度大于入渗强度而产流,这时仅表层土壤饱和.但是这类情况并非一成不变,湿润地区久旱多雨可能发生超渗产流,干旱地区的多雨季节或山区,可能发生蓄满产流,后者的原因是山地的土层薄,容易饱和.
为描述漫流过程,方程(2.2.4),(2.2.5)中R应代以I(t,x), f(t,x)这里I为降水强度,f为入渗率.对于超渗产流来说,f采用Horton方程是适合的或者说是常用的.必须注意的是仅当I>f时才有计算漫流的可能性.Wood等(1990)采用下式作超渗估计,以模拟坡面对暴雨的响应

式中tp是入渗率小于降水强度I的降水历时,tp,tc,c,Sr是与土壤性质有关的参数,tp决定产流时间.这个关系最初为Sirnpalan等建议,他们认为超渗时入渗率由表层土壤的水力传导系数K0和土壤性质、含水量等决定.
与超渗产流相比,蓄满产流的理论模型较为完备.Govindaraju和Kavvas(1991)建议取

(2.2.17)
式中,ψ(x,t)表示压力水头,当降水发生时,雨水以达西渗透规律
![]()
入渗,这时土壤水相当于地下水运动,入渗多余部分成为侧向水流而产
![]()
产生溢出.在Govindaraju和Kavvas的工作中,他们取连续流方程为:
![]()
式中,V为水流速度,hV即为单宽流量,而流速V被取作
![]()
式中,D0,α,β为曼宁数,阻力坡Sf显然为坡度S0与水位差的代数和
![]()
其次,ψ也是需要计算的
![]()
(2.2.22)
式中,Ss是土壤贮水系数,η是土壤有效空隙率,θ是含水率,c(ψ)称土壤介质含水率,取作
![]()
s是坡面上的汇源项.(2.2.22)式实际上是二维达西定律在土壤中的形式.这样求解出的坡面流不再具有运动波的形式.

图2.2.1是坡面漫流过程的观测结果及上述关系模拟的结果.从图中我们可以发现,坡面漫流有一个逐渐变深的过程,而漫流退水过程却是相当迅速的,这与河川径流的洪水波不一样,洪水波一般呈现明显的扩展性质,退水过程较长.
3.水文学近似
漫流的计算模拟是繁琐的,其机制也是较为复杂的,许多地方需要参数化处理,为此发展了基于系统论观点的水文学途径.
将整个坡面看作一个系统,坡脚的出水作为输出,设坡面是规则的,以s表示坡面单宽蓄水,qL(t)表坡脚流量,由水量平衡原理显然有:
![]()
式中,R与L的乘积RL给出了无入渗时的坡面系统输入.Horton假设qL具有下列形式
![]()
并记QL为qe则有
![]()
式中,a,c为常数.这是以qe为控制量,s为状态量的一个非线性系统.求解了这个方程,取
![]()
则发现当c=1,2,3,4,3/2,4/3,有解析解.特别是当c=2时,降水过程中有:
q=qeth2(tqe/se)qe>0
(2.2.28)
成立.在旁侧入流为0的退水过程有
q=qe/[1+qet/se]2
(2.2.29)
式中,qe为涨水期达到的最后水量.
4.更一般的情况
在前面的讨论中,我们限制问题为一维,实际上漫流的运动受空间地形分布的影响颇大,因此需要高维模型.Akanbi等(1988)应用二维欧拉方程建模讨论漫流问题①:
连续性方程
![]()
动量方程
![]()
(2.2.31)
![]()
(2.2.32)
式中,h为水深,u,v分别为x,y向流速,S0x,S0y为x,y向流床坡降,Sfx,Sfy为x,y向阻力波,R为旁侧入流,Dlx和Dly为渗漏量,分别是u与v的正比函数.

式中,i是入渗量,求解这个方程显然要与入渗关系相联系.Akanbi等(1988)对方程引入了一组结构关系以便问题化简


式中,z0为原始流床高程,n为糙度.为求解方便他们还把问题化到运动坐标系.
Akanbi等认为对于一个干燥的地面对演,有Kostiakov关系成立:

式中,ts为地面饱和时间.
Akanbi等研究了漫流的一种特例,洪水从山口涌出,泛滥在山前平原上.这时降水已经停止,因此a=i,地面干燥,辐射状的涌出的洪水初始条件为
![]()
式中,r0为山口原点,WF是出口洪水波波速,数值模拟的结果发现山前平原上的漫流洪水以扇形展布;波形受山前地形影响明显.当“山前平原”地形受限时,在边缘部分将发展起较高的水位,当“山前平原”无限开阔时,洪水将呈典型的扇形展布,如图2.2.2所示.这一结论对我们分析山洪灾害很有意义,在沟谷地区,谷坡上水位可能高于中央沟道,造成较大洪灾损失.

最近的一些工作,建议用孤立波模拟漫流的来水,或者提出了不同地面条件下能坡与流速的关系(Kadlec,1990).这些工作为进一步研究漫流过程,特别是漫流产生的洪灾过程,提供了好的基础.
2.2.2 河川径流:洪水波
1.基本观点
坡面漫流水量最终汇入其附近的河道,产生河川径流,河川径流包括两个部分地下水提供的基流和漫流汇入产生的洪水波,洪水波的运动仍然满足Saint-Venant方程.与漫流问题相比较,河川径流(以下称径流)问题较简单,第一,一般可不考虑侧向入流,第二,问题的一维性质更为明显.径流方程一般作(文康等,1991)连续性方程
![]()
动量方程
![]()
或者写作
![]()
式中,A为断面面积,Q为断面流量,u为流速,S0为流床坡降,Sf为阻力坡.(2.2.43)式中右边第二项被称作惯性项,在洪水波运动中,它引起了附加的比降.在大河下游,没有支流和回水的情况下,一般可以忽视;多数情况下,这一项也仅有河道坡度的千分之几,因此,忽视是可能的.
利用(2.2.41),(2.2.42)可以得河道中流量水位的一般性关系

![]()
代表湿周,不再表示旁侧入流).其余的项引起洪水运动的非稳定变化,产生水位与流量非一对一的所谓“绳套”关系.显然,简化洪水波运动模拟关系的关键在于处理根号内的项,使之得到水位与流量的单值蓄池关系.
研究径流运动的另一重要目标是河段汇流时间.设断面A是流量Q,流程x的函数,并且Q也是x的函数,即有A=A(Q,x)和Q=Q(x,t)同时成立.这时连续性方程可以化作
![]()
在稳定流量的情况下,dQ=0,从而由
![]()
和连续性方程(2.2.45)得到
![]()
这样河段x内的汇流时间(注意dx/dt为稳定流量传播速度)
![]()
或
![]()
式中△Ai,△Qi分别为河段△xi的断面面积和流量增量.
2.洪水波运动的模型
1) 运动波与扩散波
(2.2.42)式是非线性的,求解困难(事实上目前尚未求出解析解),因此需要对它作简化处理.取
S0-Sf=0
(2.2.50)
并忽视惯性项,则得到运动波模型.事实上这时出现稳定均匀流,在漫流的讨论中,我们已经知道,这时水流运动满足
![]()
形式的运动方程.
若仅忽视惯性项则由
![]()
描述动量关系.并取
Sf=Q2/K2(h)
(2.2.53)
K为某一与h有关的参数则有
![]()
在此基础上注意到连续性方程,可以导出
![]()
其中
![]()
![]()
式中,B为河宽,C称为偏移系数,决定了波的定向移动,D为扩散系数,使洪水波坦化,它是一般的(线性)波动方程.对矩形河道来说,容易证明(文康,1991),无论运动波还是扩散波,均有
C=1.5u0
这里u0是稳定的均匀流流速.
2) Dooge的LCR模型(线性渠道响应模型,1978年,参见文康等,1991)
Dooge认为,任意舍弃某些非线性项可能产生较大误差,因此,他建议对原始方程在稳定状态附近作线性化,而不是先舍弃某些项.取Sf满足谢才公式,动量方程可化作
![]()
(2.2.58)
这里q是单宽流量,注意到q=uh,故有

从而得到
![]()
取漂移为q=q0+q1,h=h0+h1,其中h1,q1是漂移小量,将漂移形式代入(2.2.53)并对t求导,化简后得
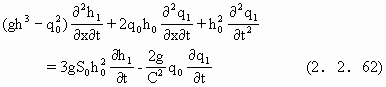
与连续性方程
![]()
配合,得到关于h1,q1的线性方程组,它是在(q0,h0)状态附近,将系统线性化的结果,相当于对原方程作摄动处理.从(2.2.62),(2.2.63)可以导出
![]()
(2.2.64)
上式左端可改写作
![]()
其中,第三、四项是波速为1.5u0的运动波项,二者的代数和为零,故有
![]()
(2.2.65)
![]()
![]()
(2.2.66)
这是以
![]()
为扩散系数,以
C=1.5u0
(2.2.68)
为波速的波动方程(扩散波方程).这就是说,Dooge的LCR模型是在均匀稳态流上面加上了一个小的扩散波,它的波形以(2.2.67)形式弥散,但关系(2.2.67)可以化作
![]()
式中,F是弗劳德数,由F的意义知洪水波弥散的条件与流态有关.
3) 马斯京贡(Musxingum)的水文学模型
最常用的洪水波计算是水文学方式而不是水力学方式的.在水量平衡的条件下,河段内的蓄量s与上下游之间满足微分方程
![]()
式中,I与Q分别为上游来水量与流入下游水量,马斯京贡认为在稳定态附近蓄量s与I,Q有关系
s=K[wI+(1-w)Q]
(2.2.71)
式中,w为权系数,K为比例参数.合并(70)与(71)式,得
![]()
这样可以得到一差分方程
Qk=-a1Qk-1+b0Ik+b1Ik-1
(2.2.73)
用于预报下游获得的水量.式中k是离散时间,a1,b0,b1是系数,差分处理方式不同,a1,b0,b1有不同的形式,最常见的是中心差分方式.
由于马斯京贡模型较为简单,而且其离散采样可由上下游测站完成.故这一模型得到了广泛的运用,并发展了关于它的众多理论.Dooge等发现马斯京贡模型与LCR之间存在着联系.当F→0时,权系数w→1/2~h0/3S0L0,这里L0是河段长.
本文标题:地表过程:漫流与径流-水文过程
手机页面:http://m.dljs.net/dlsk/lidi/21139.html
本文地址:http://www.dljs.net/dlsk/lidi/21139.html

