5．12 数字图象处理

　

    图象的含意很广，所有记录在纸上，拍摄在照片上，显示在屏幕上具有视觉效果的画面都可称图象。通常随记录方式不同，将其分成模拟(analog)图象和数字(digital)图象。前者的图象信息是通过光电强弱的连续变化来记录的；后者是通过离散的象点数值记录的。通常所说的图象处理是指数字图象处理，对模拟图象的处理是通过模数(A/D)转换装置，将其转成数字图象再行处理的。

    从地理信息系统的角度看，数字图象处理涉及对栅格数据结构的地理信息系统的分析处理以及地理信息系统和遥感的结合等方面。

    5．12．1 图象数据

    一、图象的表示

    数字图象通常是把一幅连续图象进行等距离采样，形成一个N×M点阵的离散值。图象采样及量化就是图象数字化的过程。这种表示同地理信息系统中栅格数据结构是一致的，数字图象中矩阵点阵中的最小单元称象素或象元，对应于栅格结构地理信息系统中的最小单元栅格。

    对连续图象进行采样和量化后，可表示为：

    这里，关键是确定离散点N与M值，及每个象素所表示二进制位数G。通常N，M，G都取成2的幂次数，如取N=1024，M=1024，G=8等。在单色图象中，每个象素的明暗程度用灰度级来表示，考虑到肉眼的分辨率及图象质量，典型情况用28=256个灰度级。即每个象素包含8个位面用一个字节来表示。

    在彩色图象中，每个彩色图象分成红、绿、蓝三种单色图象，每色具有256级灰度，因此，每个象素要占3个字节，即24位面。在图象处理中，对彩色图象的处理实质上是对红、绿、蓝三种单色图象分别进行处理。

    二、图象数据文件格式

    图象是由排成矩形点阵的象素组成的。因此，记录一幅图象时，必须同时记录下各象素在点阵中的位置及象素的灰度值。通常用象素在文件中的记录位置来隐含图象点阵位置，因此，只需记录各象素数据的灰度值。由于图象点阵是二维的，为了用一维形式记录二维图象，通常采用的办法是将各行象素数据首尾相连。

    使用图象数据需注意其格式，现有许多不同图象数据格式，其中有些格式已广泛流行，通常各种图象软件均支持它们，如 BMP， TIFF， GIF格式，也有支持图形软件的DXF格式等。

    BMP(BIT MAP)格式是Windows环境中一种图象交换标准，通常在Windows环境中运行的图形图象均支持该标准。

    TIFF(Tagged Image File Format)格式是由Aldus和 Microsoft公司联合开发的，是目前广泛流行的一种多变图象标准，在TIFF文件中图象信息的存放是机动多变的。因此，对TIFF文件格式解码时要注意这种情况。

    GIF(Graphics Interchange Format)格式是一种公用图象文件格式标准，但它的版权归CompuServe公司所有。在GIF格式中图象数据一律采用LZW算法压缩。

    DXF(Drawing Interchange Format)是一种绘图交换格式，它广泛支持各种CAD程序，起源于Autodesk公司的AUTOCAD上。有关这些格式详细情况可参阅有关书籍。

    三、图象直方图

    图象处理的实质是对图象数据中各个象素数据与相邻元素之间关系进行计算处理。图象直方图(histogram)是按灰度值来显示图象、象素频度的统计图。对一幅4×4图象其灰度值如图5-55(a)所示，则它的直方图如5-55(b)所示。

    根据直方图可以大体了解图象数据的灰度分布。直方图已广泛用于图象处理中，如图象二值化，图象的增强处理等。

    5．12．2 图象的增强(Enhance)

    图象增强是指利用数学方法和变换手段提高图象中对象物和非对象物的对比度及图象清晰度。这里的对象指图象中需要寻找和研究的内容，如通过突出边缘勾画出河流湖泊的边界，描绘地块的轮廓及去除图象中噪声等。

    增强处理后的图象，突出了需要部分的信息，削弱了不需要部分的信息。

    图象增强的方法很多，随增强目的不同可选择不同方法，下面就改变灰度等级提高对比度，突出边缘锐化图象及消除噪声平滑图象方面加以简介。

    一、图象灰度增强

    1．对比度变换。对比度是图象f(x，y)中最大灰度值和最小灰度值之比。对比度变换是为了改善图象清晰度而作的改变各种灰度值的灰度范围的变换。常用的变换有直线变换，分段直线变换，对数变换及指数变换等。以实现局部图象灰度范围的扩大(图象拉伸)和缩小(图象压缩)。图5-56列出几种对比度变换方法，其中x轴表示原图象的灰度范围，y轴表示变换后图象的灰度范围。

    2．直方图均衡。直方图均衡是灰度增强的另一类算法。通常一幅对比度小的图象其直方图分布一定集中在某一比较小的灰度范围内。当一幅图象具有平坦均匀分布的直方图时，可得到较好的视觉效果。所以，对直方图集中在某一区域的图象，进行直方图均衡处理是增强图象灰度的一种较好方法。如图5-57所示。

    二、边缘增强

    图象的边缘增强也称图象的锐化。其目的是突出图象中的边缘或某些亮度变化率大的部分。常用下列算子：

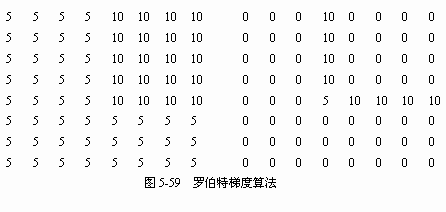
    1．罗伯特(Roberts)梯度算子。梯度反映了相邻象元之间灰度的变化率，在图象的边缘处，必定具有较大灰度梯度值。

    用交叉差分法求相邻象元之间灰度变化率的方法，称罗伯特梯度。若图象为f(x，y)表示为

    |grad(f)=|f(i，j)-f(i+1，j+1)|+|f(i＋1，j)-f(i，j＋1)|

    用罗伯特梯度算子运算的实质是交叉地求对角方向象素之间灰度差的和，作为该象素的值。对一幅图象从左到右，从上到下扫描一遍，求出各点梯度产生梯度图象达到突出边缘的目的。图5-59为用罗伯特梯度计算后图象轮廓的增加情况。

    2．拉普拉斯算子(Laplace算子)。上面所说的梯度运算是通过图象上空间灰度的变化率来增强边缘。拉普拉斯算子求的是图象空间灰度变化率的变化率，它不检测均匀变化率，其目的是更加突出灰度值突变的位置。

    若图象为f(x，y)，拉普拉斯算子的一般形式为：

    对于数字图象，拉普拉斯算子的离散形式为：

    用模板表示如图5-60(a)所示。

    为了增加图象的高频分量产出拉普拉斯图象增加算子，其模板如图5-60(b)所示。

    三、图象的平滑和去噪

    通常图象的视觉质量可以从图象的分辨率，图象中物体边缘的锐度及图象中噪声干扰大小等确定。产生噪声原因是各种各样的，有电的、非电的(如胶片中颗粒噪声)、图象数字化时量化噪声和光电元件的随机噪声等。图象处理的一个重要方面是用平滑滤波方法，以去除图象中的噪声。

    1．图象平滑处理用来保留图象的低频部分，削弱高频部分，经过平滑处理后的图象相当于经过了一个二维低通滤波器。

    线性平滑处理是把图象中每个象素的灰度值用它的邻域灰度的均值来代替。邻域的大小可以为3×3，5×5，7×7等。对于3×3的模板其系数

    这意味着图象上每个象素用它邻近(包括它本身)的9个象素的平均值取代。这种处理，在除噪声的同时，降低了图象的对比度，使图象变得模糊。为此可选用如下模板系数，以便在去噪的同时较好地保留原图象的对比度。

    在非线性平滑处理中，并不把所有象素用它的邻域平均值代替，而是取一阈值T，当象素的灰度值与邻域平均值之差大于阈值T时，以均值代替，以消除一些孤立的白色或黑色噪声点。它对图象的细节影响不大，当然对物体边缘可能会带来一些失真。其变换式为：

    2．中值滤波。中值滤波是在以象素为中心的M×N邻域范围内取灰度中值代替该象素的值，以实现“去噪”和平滑图象的目的。

    设有一个一维序列x1，x2……xn，用长度为m的窗口(m为奇数)，

    中值滤波是以中值代替平均值，达到滤波作用。同时又可保留某些亮度的起伏，不致于使图象灰度变化削得太平坦。

    窗口运算与模板运算相同，即从左到右，从上到下按列按行扫描全图，一遍完成。

    例如：下面一个4×4图象，用1×3窗口作中值滤波，其结果(最左最右列保留原值)如下所示：

    上式中可知，原图中冒尖噪声9被除去了。

    实际上，为了使中值滤波得到较理想的效果常需要采用不同形状和大小的窗口。

    5．12．3 图象几何校正

    在图象生成过程中，由于各种原因会产生几何失真。就卫星遥感图象而言，分系统失真和非系统失真。系统失真往往是由于多光谱扫描镜线速不匀，检测器采样延迟造成的波段不配准以及卫星前进运动造成扫描歪斜等原因产生。非系统失真是由卫星飞行高度，速度姿势的变化以及地球自转等因素引起的。

    为此在图象处理时，需要以一幅图象为基准，去校正另一幅图象。

    几何校正的实质是根据两幅图象中一些已知对应点(称控制点)建立函数关系式，即将被校图象按标准图象的几何位置校正。最后使失真图象中每个象素点都可在标准图象中找到对应点。

    在地理信息系统中，用数字化仪或扫描仪输入同一地区几幅图后，在分析处理中需将几幅图配准，这也是一种几何校正。在执行校正中，要求精度越高，算法越复杂。所以应根据实际要求选择合适精度。

    下面介绍两种常用几何校正方法：

    1．三角形线性校正。这种校正是一种线性校正，适合于线性失真的校正。如地理信息系统中，当输入多幅同一地区图时，需进行的配准。

    在遥感中所述的几何失真，通常是非线性的，但在局部区域内可看成线性的。因而可将标准图象和被校图象之间的对应点划分成一系列三角区域，把三角形顶点作为3个控制点，分别进行校正。

    假设三个控制点在被校图中坐标分别为(x1，y1)，(x2，y2)，(x3，y3)在标准图中其对应坐标为(u1，v1)，(u2，v2)，(u3，v3)可建立6个方程：

    从中求出6个系数a，b，c，d，e，f，则认为三角形区内任意点均满足x=au＋bv＋c，y=du＋ev＋f。这种校正用在非线性失真情况下，控制点越多，分布越匀，三角区面积越小，则精度越高。

    2．二元多项式校正。二元多项式校正把标准图象的空间坐标点(u，v)同被校正图象的坐标点(x，y)之间，用二元多项式来描述，可以是二元一次、二次、三次及更高次的表达式。对二元二次多项式，其表达式为：

x=a00+a01v+a02v2+a10u+a11uv+a20u2

y=b00+b01v+b02v2+b10u+b11uv+b20u2

    计算前，首先找出两幅图象的对应点，称控制点，然后用最小2乘法从已知控制点坐标求出未知系数，从而得到上述关系表达式的具体表示。最后，用上述关系式对图象进行校正。

    控制点的数量，由方程未知数确定。如上述二元二次多项式有12个系数，需列出12个方程，所以需选择6个控制点。控制点在图上位置应该均匀，并要注意边界位置，以防图象校正不能满幅。

    5．12．4 图象的分割(Segmentation)

    图象分割是根据图象的某种特性把不同目标区分出来。它实质上是一种标记过程，即把一幅图按一定规则划分出感兴趣部分。图象分割的办法很多，很难规定出一套准则说明分割得好坏，只能从效果判别。这里简单的介绍两种图象分割方法。

    一、取阈值法

    这种方法，用预先取好的灰度阈值逐点分割各象素。这种分割法的关键是阈值的选取。以二值图象为例，设图象f(x， y)，具有直方图如图5-62所示，则按阈值t分割将得到二值图象fT表示为：

    选取阈值的方法很多，通常借助图象直方图来确定。对于呈双峰的直方图，通常，取谷的中间值作为阈值，如图5-61(a)所示，也可求图象灰度梯度值，取梯度最大处作为阈值，如图5-61(b)所示。有时，在图象不同区域需取不同的阈值称动态阈值来分割图象。

    二、分—合图象分割

    这种算法是基于四叉树数据结构进行的。首先按四叉树数据结构将图象进行分割，然后再按区域相邻数据结构进行合并。其步骤如下：

    (1)将原始图象选择某种编码构建四叉树，如图5-62(a)所示。

    (2)自某一中间水平开始，在各相应块中，进行灰度值一致性测量。若一致性测量为假的块，一分为4重新编码，这样重复测试直到所有各块一致性测量为真为止。

    (3)自同一中间水平开始，测试属于同一父节点的四块。若它们的一致性为真，则合并这4块，重复操作，直到不再存在可合的属于同一父节点的四块为止。其结果如图5-62(b)所示。

    (4)利用区域相邻数据结构，对相邻的大小不一或虽然大小一样，但不能合为一个父结点的区域进行一致性测试，将一致性为真的区域合并，这样反复重复合并直到不再存在可合的区域，从而形成图5-62(c)所示目标。

    分合算法起始于一中间层次，若自最顶层开始就成自上而下分割算法；反之，若从最低层开始，就变成自下而上的合并算法。

5．12．5 图象的细化

    图象的细化是指将图象上直线，曲线和文字等几何元素的线条，沿着中心轴将其细化成一个象素宽的线条。细化意味着删除一部分象素，使图象的连接性不变，即不改变原图的拓扑关系，保证各连接部分不分离，不结合，对原图孔不生成，也不消灭。此外，保留原图关键部分如各线的端点和突出部分等。

    细化处理是图象处理中一种重要的处理方法，对不同对象常常可选择不同处理方法，以获得好的处理效果。这里介绍两种处理方法：

    一、细化方法一

    该方法最初用于加拿大地理信息系统CGIS中，以后也有一些系统使用类似的方法。

    假设细化前所有栅格元素为二值数据，即背景为0，图象值为1。其细化步骤如下：

    1．利用2×2求和算子沿着图象扫描方向扫描，用求和所得值V值代替原值。即：

    V=f(i，j)＋f(i-1，j)＋f(i-1，j＋1)＋f(i，j＋1)

    也就是aij象素值是该点象素值加上北，东北，东三个相邻象素值之和的值V，其值可为0，1，2，3，4。如图5-63(c)是图5-63(b)的V值图。

    2．保留最大V值。即删去其他值，保留最大值，同时保持线的连通性，由这种方法保留的最大值常处于线的中间位置，如图5－64所示。

    3．用链码表示原图。对细化图用3．3中所述的链码来表示。从起点开始追踪，记下8个方向链码，然后开始下一条线的追踪，重复上述过程直到所有线段追踪完毕为止。

    本细化方法处理简单，但若原始图形较宽时，会出现多个最大值并列的现象，因而不能一次成功。

    二、细化方法二

    该方法使用3×3模板，所用定式化模板如图5－65所示。中心栅格有8个邻域，其组合应有28种不同格式，考虑到其相对位置差异只是转90°，180°，270°或互为镜象反射方式，这样得到A，B，C，D，E，F，G共7类模板，各模块中×符号代表数值2或3。

    这里约定原图象的背景值为0，图象象素值为3，即细化前所有栅格元素已二值化。现沿图象扫描方向搜索，将当前象素周围3×3领域内的象素与定式化模板进行比较和处理。若当前象素值为aij，处理结果后当前象素值将赋予新值f(aij)。f(aij)由下列条件决定：

    1)若aij≠3，或者aij的邻域为A或B模板形式时，f(aij)=aij；

    2)若aij=3，且aij的邻域为C模板形式时，f(aij)=2；

    3)若aij=3，且aij的邻域为D或E模板形式时，f(aij)=1；

    4)若aij=3，且aij的邻域为F或G模板形式时，f(aij)=0。

    将原图象按扫描方向，对逐个象素进行处理后，各象素的值将是0～3中的某个值。此时的象素值具有以下意义：

    0：为背景象素；

    1：表示有一个以下相邻图形象素；

    2：两侧各有一个相邻图形象素，表示线上点；

    3：有3个以上相邻图形象素，表示结点。

    该方法只需进行一次处理，能实现细化，但它只适用于闭合曲线，对开曲线应用此法，会导致错误的细化结果。

　　本文标题：数字图象处理
　　手机页面：http://m.dljs.net/dlsk/gisjiao/10628.html
　　本文地址：http://www.dljs.net/dlsk/gisjiao/10628.html